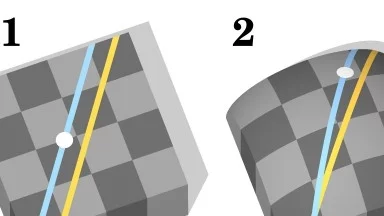
Неевклидова геометрия е термин, обединяващ хиперболичната и елиптичната геометрия, които се разграничават от евклидовата геометрия. Основната разлика между евклидовата и неевклидовата геометрия е естеството на успоредните прави. В евклидовата геометрия, ако са дадени права l и точка A, нележаща на l, то през A може да се прекара само една права, успоредна на l. В хиперболичната геометрия съществуват безброй много прави през A, успоредни на l, а в елиптичната геометрия не съществуват паралелни прави.
Още: Националната библиотека пази най-малката книга с Господнята молитва у нас (ВИДЕО)
Още: Роден е Димитър Хаджигеоргиев, български композитор
Друг начин да се опишат разликите между тези геометрии е следният: Нека са дадени две прави в една двумерна повърхност, които са перпендикулярни на трета права. В евклидовата и хиперболичната геометрия тези две прави са успоредни. В евклидовата геометрия обаче тези две прави остават на еднакво разстояние една от друга, докато в хиперболичната геометрия те се отдалечават една от друга, увеличавайки разстоянието помежду си с отдалечаването от точката на пресичане с общия перпендикуляр. В елиптичната геометрия линиите се приближават една към друга и на края се пресичат — следователно в елиптичната геометрия не съществуват успоредни линии. В първите години от професурата си руснакът Николай Лобачевски се занимава усилено с евклидова геометрия, правейки опити да докаже Петия постулат на Евклид. През 1823 г. представя ръкопис на учебника си по геометрия, в който обаче изложението чувствително се различава от традиционното. Говорейки за Петия постулат, Лобачевски изтъква, че той няма нужда от строго доказателство; нещо повече, приема, че постулатът не е верен и на тази основа изгражда нова аксиоматика на геометрията. Съдбата на ръкописа е печална - даден за анонимна рецензия на Николай Иванович Фус, той бива остро разкритикуван. Лобачевски прави втори опит през 1836 г. На 23 февруари излага идеите от книгата си "Съкратено изложение на началата на геометрията" ("Сокращенное изложение начала геометрии") пред факултетното събрание. Днес тази дата се приема за рождена за неевклидовата геометрия, която самият Лобачевски нарича "хиперболична". Но и този му ръкопис не е публикуван веднага - едва през 1829 - 1830 г. първата част от него излиза в "Казански вестник". Евклидовата геометрия се моделира от понятието „равнина“. Най-простият модел на елиптичната геометрия е сфера, където правите са големи окръжности (като екватора или меридианите на един глобус), а срещуположните точки се идентифицират (смятат се за съвпадащи). Дори след трудовете на Лобачевски, Гаус и Бояй остава въпросът, дали съществува такъв модел за хиперболичната геометрия. Отговорът е намерен от Еудженио Белтрами през 1868 г., който доказва, че повърхнина, наречена псевдосфера, има кривина, подходяща за моделиране на хиперболичната геометрия. Работата му е пряко основана на тази на Риман. Значението на труда на Белтрами е в показването, че хиперболичната геометрия е логически непротиворечива, ако евклидовата геометрия е такава. Развитието на неевклидови геометрии се оказва много важно за физиката през 20 век. При ограничението на скоростта на светлината сумирането на скорости изисква използването на хиперболична геометрия. Айнщайновата теория на относителността описва пространството като, общо взето, равно (т.е. евклидово), но изкривено елиптично (т.е. неевклидово) в области около места, където има наличие на материя. Тъй като Вселената се разширява (виж константа на Хъбъл), пространството, където няма материя, може да се опише чрез хиперболичен модел. Този вид геометрия, в която кривината се променя в различните точки, се нарича риманова геометрия. Има и други математически модели на равнината, в които постулатът за успоредността не е валиден, например в равнината на Ден, състояща се от всички точки (x, y), където x и y са крайни сюрреални числа.
Източник: Уикипедия